選択した画像 平方根 公式 中学 323986

中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 根号を含む複雑な式は、なるべく簡単な形に変形してから値を代入し、分配法則や乗法公式を使って√を含む式を計算する練習問題プリントです。计算平方根和牛顿迭代法 在读研究生的时候，我去过北京师范大学东门的书店，看了看一本中学教材，介绍了古代巴比伦人计算平方根的算法（只是阅读材料，并没有深入到原理），我当时不知其所以然，兴趣淡薄，也只是随手翻翻。 说起来古巴比伦人 スポンサーリンク 数学分数や小数の平方根（へいほうこん）って、どうやって求めるの？ 平方根 中3 中学数学 数学おじさん まずは前回の復習をサクッとしておくと、 平方根を求めるときの考え方を学んだんじゃ 平方根を求める手順は、以下

トップ100 因数分解公式中学 子供のための最高のぬりえ

平方根 公式 中学

平方根 公式 中学-中3数学の 「平方根」 ですね。 大丈夫、安心してください。 初めて出る言葉が多いので、 戸惑ってしまう中学生も 多いのですが、 以下でバッチリ解決できます。 得点アップ法をまとめるので、 丁寧に読んでみてくださいね！ 「2乗になる数」って 中学数学平方根「整数になる自然数n」の簡単なやり方&丁寧な解説！ 塾長 年8月21日 / 年9月17日 そして、みんなやる気があるんですぐ出来るようになるんですよ。

中学数学公式中学手绘初中数学公式png图片素材免费下载 图片编号 Png素材网

 中学3年生で学習する二次方程式ですが とにかく解き方が多い！ 今回の記事では、これらの計算方法についてイチから解説をしていきます。 それぞれの練習問題も用意しているので この記事を通して二次方程式を完全マス 今回は解の公式を使った解き方について行いたいと思います。それではみていきましょう。 解の公式 今までやってきた2次方程式の計算問題は全部「解の公式」で解けるんですが, この公式はとても"面倒くさい"し, 間違えやすい。なので, 他の解き方でいけるなら, そっちで解いた方が良い平方根の覚え方 2、3、5などの平方根の値は暗記すると便利です。平方根の値は、物理学や工学で使うからです。語呂合わせを下記に示します。 上記の平方根は、最低限覚えるべきでしょう。 平方根の公式と問題 平方根の公式を下記に示します。

平方根 展開の公式を使ったルートの計算、7題の演習にチャレンジだ！ 問題を使って徹底解説！ 平方根 125 中学応用整数部分、小数部分の求め方！中学で覚えておきたいのは以下の5つ！ 平方根を考えないといけないので注意が必要です。 平方根 展開の公式を使ったルートの計算、7題の演習にチャレンジだ！平方根の足し算と引き算は、 ルートの中身が同じ数を1つにまとめます。 パッと見は中身が異なる場合でも、 ルートの中身を簡単にすると同じになるケースもある ので、ルートの中身を可能な限り簡単にしてから足し算・引き算を行います。 50 18 を計算

中学3年生用の数学･問題ソフトです。 平方根利用で解く⇒ 平方根利用(発) 平方根利用(分数)⇒ ax^2=b(分数) ax^2=b(有理化) ax^2=b(有理化2) 解の公式で解く⇒ ルート・平方根の計算方法・仕方の3つのコツ ルート計算のコツはつぎの3つだ。 ルートを簡単にする 足し算・引き算はべつもの 分母は有理化しとく 練習問題をといてみよう。 つぎのルートの計算をしてください。 √8 √2分の5 – √3 × √5 コツ1平方根を計算することは、x 2 =aとなるxの値を求めることになります。 また、中学校では a が0以上の数である場合のみを勉強します。 なぜなら、2乗して負の数になる数は存在しないからです。 ※ 高等学校では、2乗して負になる数も学習します(虚数）

计算某数平方根的公式和迭代公式 腾讯新闻

一元二次方程的求根公式 知网百科

 中学全学年 数学の平方根についてです！ ♡、コメント、フォローよろしくです！ 数学 math このノートが参考になったら、著者をフォローをしませんか？ 気軽に新しいノートをチェックすることができます！ 方法/步骤 1/3 分步阅读 能简化的根式先尽量简化。 该信息非法爬取自百度经验 2/3 再将根数相乘，得出结果。 3/3 最后把任何可以简化为完全平方数的数分离出来。平方完成 平方完成 \(2\) 次方程式は、因数分解によって解くことができる。 非常に重要なことを学びましたが、これで万事解決ではありません。 次の \(2\) 次方程式を解いてみましょう。 \(x^26x1=0\)

平方根の計算 やり方は をつけてルートをつけよう 中学や高校の数学の計算問題

ユニーク中学1 年数学方程式 ぬりえ壁紙hd

 平方根も因数分解もできないなら 解の公式！ \ (x^28x4=0\)、\ (2x^26x3=0\) など。 それぞれの解き方を何度も練習して自分のモノにしてください！ このページでは、中学3年生の数学で押さえておきたい重要ポイントである "多項式の計算" 、 "因数分解12 12 は平方数ではありませんが・・・ √12 = √4× √3 12 = 4 × 3 なので √12 = 12 = 2 2 ×√3 = 2√3 × 3 = 2 3 のようにします。 根号の中の数を、できるだけ小さくすることがルールです。 例えば √0 = 2√50 = 5√8 = 10√2 0 = 2 50 = 5 8 = 10 2 のように、同じ値で 筆算をつかった平方根の求め方を、 開平法 とよんでるよ。 中学数学では勉強しないんだけどね。 えっ。 どんなときに開平法をつかうかって！？ つぎの3つのときが多いよ。 デカい数の平方根を求めるとき;

数学平方根价格报价行情 京东

ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく

 平方根 中学3年で学習する単元ですね。 「√」 この記号（根号）には、かなり苦労したのではないでしょうか？ 高校数学では、複雑な計算問題がかなら出てきます。 問題を複雑に見せている要因の一つは、この平方根です。 √を含む四則演算;

平方根的符号 数学根号必背口诀 无师自通网

数学公式求和复数平方根 数学png图片素材免费下载 图片编号 Png素材网

干货 初中数学 数的开方 知识点梳理 知乎

初中数学 求平方根问题不会做 总出错 一节课帮你搞定

春中学教材全解七年级数学下沪科版上海科技版7年级 初一下薛金星主编教材同步辅导图片 高清实拍大图 苏宁易购

高中数学公式定理知识汇编 建议家长收藏 高中学霸的高分秘笈 每日头条

1

平方根 立方根 我的网站

算术平方根 2501的近似计算 百度经验

公式背會數學不難 中學數學提前學 雪花新闻

平方根公式 搜索结果 哔哩哔哩 Bilibili

初中数学 求平方根问题不会做 总出错 一节课帮你搞定

数学平方根 初二数学 上 知识点 平方根 尚书坊

I与负数的平方根 知乎

初中数学 求平方根问题不会做 总出错 一节课帮你搞定

169的平方根公式 搜狗搜索

トップ100 因数分解公式中学 子供のための最高のぬりえ

完全平方公式提升练习题 松鼠文库

平方根公式计算过程 初中数学平方根的计算公式怎么算更简洁 学习岛

公式数学中学数学联盟 创造性初中数学公式png图片素材免费下载 图片编号 Png素材网

平方根公式计算过程 初中数学平方根的计算公式怎么算更简洁 学习岛

初中三年数学公式定理总结 太有用了 中学 网易订阅

中学生数学公式 シモネタ

平方根公式计算过程 初中数学平方根的计算公式怎么算更简洁 学习岛

数学计算机图标平方根公式数学表示法公式png图片素材免费下载 图片编号 Png素材网

中学七年级数学下册6 1 平方根练习卷 无答案 新版 新人教版试题 爱问共享资料

上海慧用信息科技有限公司 数据分析中的五大思维方法

最全初中数学公式表 初一到初三都能用 楠木轩

中学数学章节教学工作计划下载 Word模板 爱问共享资料

算术平方根 1445的近似计算 百度经验

1 10的平方根口诀表 西瓜视频搜索

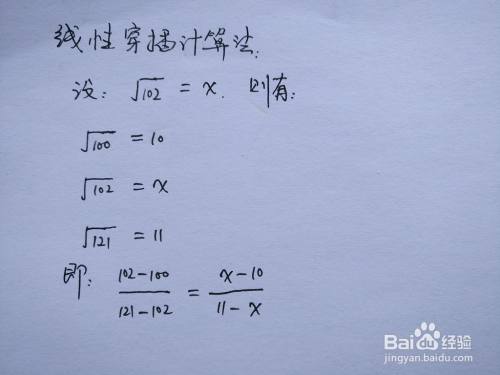
算术平方根 102的近似计算 百度经验

1 10的平方根口诀表 西瓜视频搜索

根号公式大全7年级 西瓜视频搜索

中学３年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

完全平方根公式 搜狗搜索

中学数学 平方根の利用 ママ塾ノート

初中数学 求平方根问题不会做 总出错 一节课帮你搞定

初中数学公式大全 百度经验

数学欧式公式纸数学各种公式png图片素材免费下载 图片编号 Png素材网

腾讯视频

4

完全平方公式提升练习题 松鼠文库

中学３年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

1 10的平方根口诀表 西瓜视频搜索

一元二次方程公式大全

数学联盟数学中学公式 手绘初中数学公式png图片素材免费下载 图片编号 Png素材网

初中开平方什么时候学的 初中什么时候学平方根 三人行教育网 Www 3rxing Org

数学平方根 初二数学 上 知识点 平方根 尚书坊

平方根公式计算过程 初中数学平方根的计算公式怎么算更简洁 学习岛

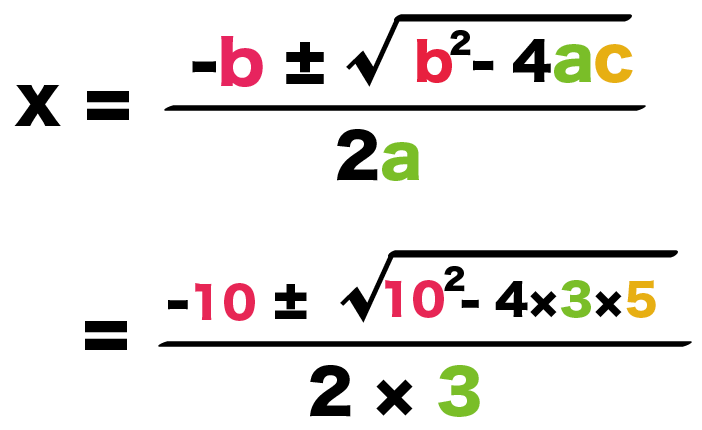
簡単計算 解の公式の問題のやり方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく

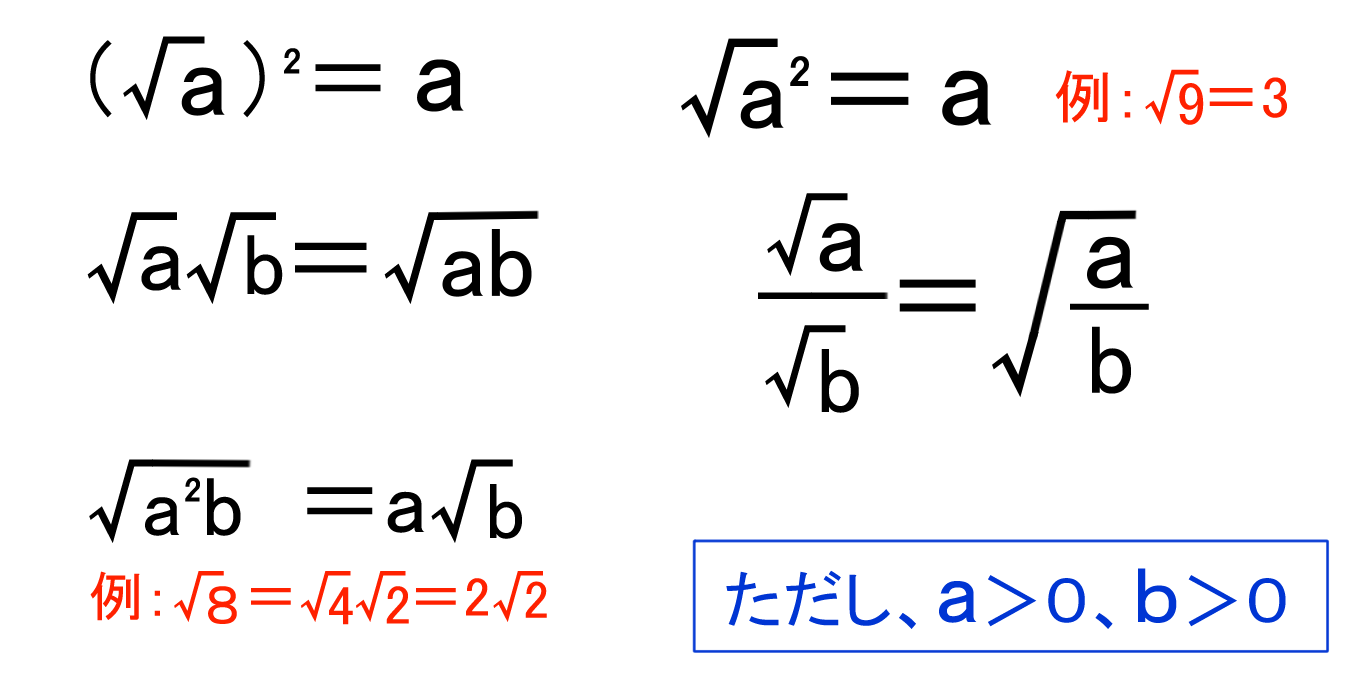
平方根 1 基本のルール バカでもわかる 中学数学

初中数学常用公式表 小初高题库试卷课件教案网

广告传媒 中学数学多媒体备课参考下载 在线阅读 爱问共享资料

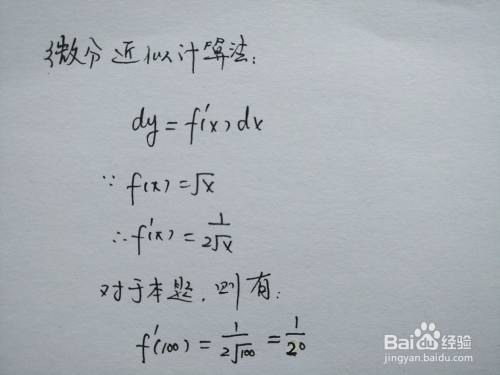
算术平方根 102的近似计算 百度经验

平方根公式 搜索结果 哔哩哔哩 Bilibili

计算某数平方根的公式和迭代公式 腾讯新闻

わかる授業動画 中学３年数学 平方根 第２３回 と基本公式 のある基本公式の使い方 A B C D Ac Ad Youtube

衡中数学老师真牛 暑假熬夜整理初中数学公式 定律 抓紧收藏 定理 不等式 网易订阅

各类教育文章分享 中学数学术语中英对照 分类整理

第一章代数 三角公式与初等代数

初中数学平方根的计算公式 初三网

ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく

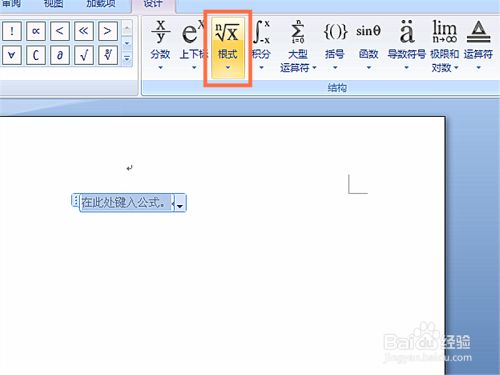
如何在word文档中输入平方根 百度经验

169的平方根公式 搜狗搜索

初中数学求算术平方根 有人秒出答案 有人无从下手 原因在这儿

1

初中三年数学公式定理总结 太有用了 纠错

中学数学 二次方程式の解き方はこの3パターンだけでok 平方根 因数分解 解の公式 楽スタ

浙教版七年级上册 0的平方根是几 负数有平方根吗 网易公开课

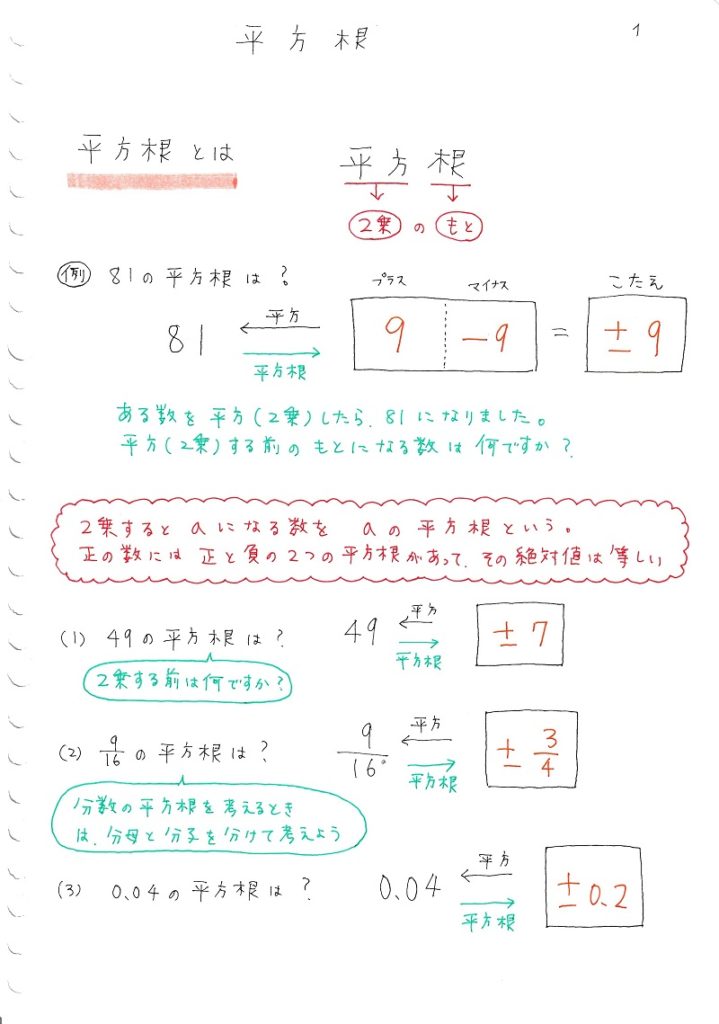
中学数学 平方根 ママ塾ノート

中学数学公式中学手绘初中数学公式png图片素材免费下载 图片编号 Png素材网

初中数学求算术平方根 有人秒出答案 有人无从下手 原因在这儿

初等数学题解 求平方根 Wx5dc22f0fa8661的技术博客 51cto博客

平方根公式 搜索结果 哔哩哔哩 Bilibili

3

初中数学 平方根的易错题 哔哩哔哩 つロ干杯 Bilibili

平方根表 平方根表 Square Root Table 常用數表之一即一 百科知識中文網

为什么要研究 1的平方根 知乎

中学数学3年 いろいろな平方根の計算 平方根と式の値 受験の月

平方根和算术平方根的区别 初三网

平方根 精品解析 小初高题库试卷课件教案网

牛顿迭代法求平方根 C Flybird的博客 Csdn博客

公式数学方程中学定理 手绘初中数学公式 三角艺术png剪贴画蓝色 免抠素材下载 图片id 其它元素 Png素材 素材宝scbao Com

黑龙江省130名数学老师扎堆 光华 切磋 技艺 新浪黑龙江 新浪网

华裔教授发现二次方程 极简 解法 丢掉公式 全球教科书可能都要改了 Mobeae43b的技术博客 51cto博客

1到100平方根口诀表 西瓜视频搜索

平方根和立方根 万图壁纸网

干货 初中数学 数的开方 知识点梳理 知乎

数学平方根 初二数学 上 知识点 平方根 尚书坊

2

高中面积公式大全图 搜狗图片搜索

ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく

初中数学公式大全 百度经验

干货 初中数学 数的开方 知识点梳理 知乎

二次根式化简的典型题

初中数学 算术平方根与平方根的区别与联系 容易混淆的知识点 哔哩哔哩 つロ干杯 Bilibili